spreadsheetjournalism

They may not be chewing this one over in your time zone, but Europe’s horsemeat scandal has frozen mouths in mid-mastication Continent-wide; and apart from the fusillade of equine-charged wisecracks riddling the Twittersphere, the scandal has tossed a bone of contention to consumers and politicians, two constituencies quick to register a beef with food purveyors.

Ok – now that I’ve gotten my jokes out of the way, let us redirect our pun-addled sensibilities to a most instructive and timely site, http://ratings.food.gov.uk/open-data/en-GB, a UK-based directory of findings that applies the national Food Hygiene Rating Scheme to thousands of food establishments (including pubs, hospitals, take outs, etc., in addition to restaurants) in England, Wales, and Northern Ireland organized by local governmental authority (Scotland works with its own scheme).

Scaling the establishments in ascending order of salubrity from 0 to 5, the Scheme site posts XML-rendered, oft-updated files which swing smoothly into Excel format. To download a file for a selected authority, right-click the English language link beneath the Download umbrella column and select Save Target As…Rename the file as you wish, but preserve the XML format. For illustration purposes, download the file for London’s Kensington and Chelsea authority, an area described in a local newspaper as Europe’s wealthiest (I can’t link it to you here, because WordPress can’t digest the XML format).

Once in Excel, you can open the file via the by-the-book route: Data tab > From Other Sources in the Get External Data button group > From XML Data Import. Go with the defaults greeting you in the ensuing dialog box, and your data are spreadsheet primed, in row-banded table form (an access alternative: simply initiate the standard Open command and approve the defaults begging your consideration in the radio-buttoned dialog box).

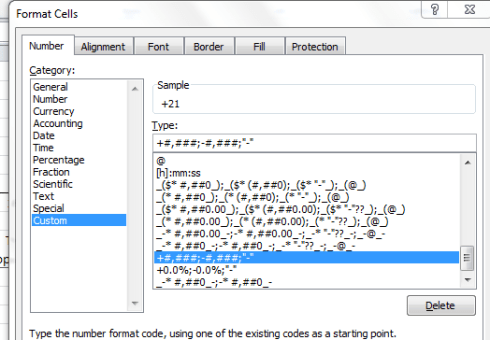
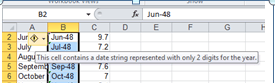
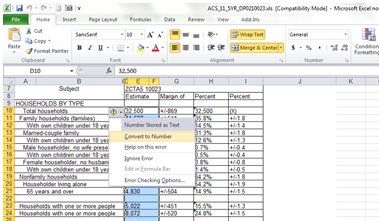
But before the data begin to comply with your analytical intentions you need to do some important preparatory work. First, the data in the linchpin L column in which the actual establishment ratings appear present themselves in the Number Stored as Text format, a most curious motif (see my January 17 post) that stands as the spreadsheet approximation to the wave-particle duality: sometimes the data behave like values, sometimes like text. But because pivot tables regard these quicksilver items as text, we need to redefine them decisively as numeric values, and we’ve done this or something like it before (note: in some Authority sheets I’ve seen the ratings are set down in columns other than L, and one sheet I’ve viewed defines its ratings in straightaway numeric terms – no manipulation required).

Select the L column and drag the vertical scroll button up to row 1, at which point you should be reunited with that cautionary exclamation mark we’ve seen elsewhere. Click it and select Convert to Number, thus quantifying the entries in the column.

Next we need to sort the column (Smallest to Largest), because a good many of the establishments either have yet to be rated or for whatever reason are exempt from any assessment, and as a result are characterized in actual text terms, e.g. Exempt. The sort should relegate the first textual item to row 1441, the position at which I usually thread a blank row, in order to detach the text data from the numerical values above. But we’re in the middle of a table, which for all its virtues sometimes outsmarts itself, to wit: insert a blank row at the 1441 position and it simply joins itself to the rest of the table, and brings along all those rows beneath it, the ones you thought you’d just unloaded. All the data in the worksheet remains in the table – with one blank row besides.

The way out of this near-Sisyphean regress is to first click the Table Tools tab > Convert to Range button in the Tools button group, and reply Yes to the prompt. Now you can interpose that blank row without repercussion.

Once you’ve burnished the data, you can do the pivot table and chart thing, e.g.

Row Labels: Business Type

Values: RatingValue (set to Average)

Rating Value a second time (set to Count)

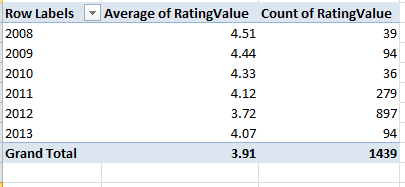
And because it takes time to vet all those establishments, how about this breakout by last year of inspection:

Row Labels: RatingDate (grouped by years)

Values: Rating Value (set to Average)

Rating Value again (set to Count)

These data point to a putative slump in collective hygiene (remember, though, that we’re examining but one local authority here, albeit a posh one), a conjecture that nevertheless must be treated with some investigative care. Have official standards been stiffened, thus forcing the averages down “artificially”, or have the more suspect establishments been subject to the more recent scrutiny? It’s hard to say, though the 897 places inspected in 2012 – a rather large number, amounting to about 62% of the total – insinuates that the inspection sequence was merely randomized. But these conjectures need to be researched. I should also add that a scan of about half-dozen authority worksheets corroborates the lower score/recency-of-inspection correlation.

To view the distributions of ratings 0 through 5 by Business Type:

Row Labels: Business Type

Column Labels: RatingValue

Values: Sum of RatingValues (PivotTable Tools tab > Options > Show Values As > % of Row Total

And additional perusals of the data can serve up piquant, near-sociological findings. Four percent of Kensington/Chelsea’s inspected establishments fell under the Takeaway/sandwich shop rubric; the comparable figure for the Tower Hamlets authority in London’s storied East End, one of the city’s poorer districts, is 12.88%, perhaps comporting with the area’s more proletarian cast – perhaps. Yet the take away/sandwich figure for London’s City – the financial center of the country, if not the world – is 21.60%, presumably reflective here of the lunch hour, eat-and-run workday. And how about the Pub/bar/nightclub percentages of all inspected establishments?

Kensington/Chelsea – 7.18%

Tower Hamlets – 9.39%

City of London – 16.20%

The ruling class likes to party.

So lots of interesting stuff out there, no? Bon appetit.

Turn to page 39 of the Centre for Investigative Journalism’s Data Journalism Handbook for this word to the hard-bitten iconoclasts of the fourth estate:

It is astonishing how many government agencies still refuse to publish information in a structured form that can be checked and analyzed. One official noted that his office had ‘previous experience of mischievous manipulation and misrepresentation of Excel and Word documents,’ and used this as an excuse to provide data only as a scanned pdf.

To which I hereby submit my standard, friendly amendment: backroom connivance aside – and connivance there may be – it seems to me that even official, ingenuous access-friendly data sets, from which all agenda and guile has been sieved, often make the work of analysis a good deal more trying than it has to be. I’ve forwarded this complaint many times, and I’ve just forwarded it again. By way of additional case in point, I’ll run the 2011 UK Census breakout of religion, the breakout drawn along perpendicular lines – that is, affiliation by coded area:

 uk Census religion 2011

(The area code field here is bound to British usage, by the way, and not the American telephonic reference.)

One-and-a-half questions beg themselves, and I’ve asked these before: 1. Again, given the lay of the data, for whom are the data intended – a readership of unreconstructed information seekers, or a research-minded cadre that might want to take the data a few more steps? And 1.5 – if the latter, where do they go from here?

That sounds like more than one-and-a-half questions, but who’s counting, and that last one could be written off as rhetorical, because the data…need work. Let’s count off some of the ways:

• The welter of blank rows interlacing the data needs to be carted away.
• That redundancy problem is back in spades. The Area Name field is recessed into three levels:  global area names (e.g., NORTH WEST), a second tier (e.g., Cheshire East UA), and when warranted a third (e.g., Cumbria/Allerdale). The result, again: the same totals being figured twice.
• Titular dispersion. That is, a heading such as Sikh Persons Number is spread across three separate cells, and failure to consolidate these will unleash major pivot table problems across the analysis. You can’t, after all, work with ten fields called Number.

And while the above irregularities aren’t irretrievably discouraging, you’ll need to make sure your sleeves are rolled up before you have a go at the sheet. And one organization that was prepared to do at least some of the heavy lifting is the UK Jewish Board of Deputies (BOD) a communal organization that brought out a report on Jewish demographics across the UK Census years 2001 and 2011. Here’s its spreadsheet:

BOD report

Of course the BOD chose not to recast the entire UK census sheet, devoting itself only to the Jewish data and their numerical relation to the areas’ general populations. Rather, it apparently resorted to a judicious copy and paste routine, mindful of the blank row and double-counting snares signaled above. Note as well that the sheet references both its 2001 and 2011 sources (though I can’t find any geographic breakouts in the S103 sheet compiled in 2001).

The results are pretty straightforward. You’ll note the conditional formats tinting the H and I columns, with red signaling a net Jewish decline in the respective areas, and green beaming an increase (and no contingent format alighting upon areas in which the population remained precisely unchanged). Note, however, that a first attempt at pivot tabling the data will incite an error message implicating faulty field names; that’s because the some header row(s) cells have been merged. You thus need to select A8:I9 and click through the Home tab > Unmerge Cells (unmerge: one more fetching Microsoft verb) option in the Alignment button group. (And yes, you’ll need to push away the totals row at 358 from the body of the data, lest you perpetrate your own double counting.)

But that won’t finish the job. Because the data’s uppermost, now–independent, row – 8 – exhibits vacancies in E8, G8, and I8, a second pivot table attempt will prod the same error message back onscreen.

There’s a bit more. Cells D10:G10’s paired titles are identical, and we mustn’t have that. I’d edit these to receive the relevant year, e.g. Total population 2011, etc. There’s also a mild-mannered formatting touch in the H column that took me a while to notice: its positive numbers are fronted by a + sign – most surely not consonant with the default setting for those values. Right-click any cell in H and you’ll open a window on Excel’s custom formatting gallery:

Custom formats can get rather fearsome, but in this case we’re told that, among other things, positive values are to be chaperoned by the +. As for the “-“? That notation describes how the value zero will appear per the format – that is, a dash in lieu of 0.

Here’s a final point. You could box out a pert pivot table aggregating the population stats by region:

Row labels: region

Values: Jewish population 2011, Jewish population 2001

But if you want to detail the collective percent changes by region, you can’t really deploy the Percent change since 2001 data even though they’re there, because the table would treat each area percent change as equally contributory to the bottom line – even as the Jewish population sizes by area are exceedingly variable. You’d need instead to wire together a calculated field, whose ingredients read something like this (I’ve called mine Percent Change):

=(‘Jewish population 2011’ -‘Jewish population 2001′ )/’Jewish population 2001’

(Again, check out the September 6 post for the how-tos if you need them.)

Follow through and garnish with the standard percentage format and you wind up with:

(And don’t ask me what a Humber is, though the name Northumbria apparently derivers therefrom – so says Wikipedia. Lots of odd place names in the UK.)

That pivot table is duly edifying, and adds materially to the BOD rendition   – but again, the data here comprise but a fractional retake of the larger, original whole. If you want to try your hand at the native UK Census sheet’s panoptic, pan-religious scan of its data, peel back those sleeves.

Last week’s cliff-hanger of a post pulled up at a familiar precipice, dangling its topical teaser from the edge of but one more data-formatting conundrum – a long skein of cells donning this – or that – format.

The cells in question skid down the B, or Dates, column in the inflation uk spreadsheet we introduced last week,s and they’re an eclectic bunch, styled in no fewer than three different formats,  fitted out across four different ranges.

Cells B2:B488 – whose adjoining C column evince RPI data and whose adjoining vacant D and E columns have yet to receive any CPI and Change in weekly pay numbers – ostensibly dress themselves in the Accounting format, a standard numeric guise:

The problem is that the data bob and weave somewhere in the interstice between numbers and text. Click the Number Format drop-down arrow and textual evidence abounds:

Authentically numeric data would appear in all their numeric finery beneath the Number rubric above, and under other headings, too. The Aug-81 you see, on the other hand, evidences something else – something decidedly non-numeric. Moreover, if you write:

=COUNT(B2:B488)

The function that counts cells in a range sporting numeric values, you’ll realize a grand total of 0. But if you multiply any cell between B2 and B488, e.g,

=B100*2

You’ll muster an actual, numeric result. Strange.

I can’t account for the bizarre duality visited upon these cells, other than to wonder if they’ve experienced some sort of mutation in the course of being spirited away from some other, primary source (that this format precisely blankets only those RPI data that precede the entry of the CPI figures at row 489 suggests an external provenance.)

In any case, a workaround is at hand. You’ve doubtless taken note of the green-notched alerts attaching to each and every cell in B2:B488; select the range and note in turn the exclamation-marked indicator and its clarifying legend:

I will confess some uncertainty over the official standing of the “date string” phrase, but that’s my problem. In any event, clicking the exclamation mark uncorks two Convert options, and because all our dates are appear to be of 20^th-century vintage, click Convert XX to 19XX (I don’t recall seeing these possibilities before either). Proceed and our problem range has been reformed into real, obedient, well-meaning dates.

You’ll be happy to know that the next 268 rows in column B are already irreproachably date-formatted, and that brings us to B757, at which the data seem to have been handed over, at least for the next 13 rows, to what the number format field in the Number button group reports as a Text format. There’s a quick fix here, too: click in I757 and enter

=DATEVALUE(B757)

DATEVALUE knocks some numerical sense into date-looking text, thus making them fit for all those pivot tables and formulas you have at the ready. Copy it down to I769, then copy those results, and apply a Paste Special to B757:B69 and take the rest of the morning off.

But the admirable efficacy of DATEVALUE got me to thinking: could we have done this same formulaic thing to B2:B489? It turns out we could have indeed; that is, we could have written

=DATEVALUE(B2) etc.

and emulate the very same text-to-bona-fide-numeric date rewrite that Convert XX worked out.

It seems the two text-laden ranges – B2:B489 and B757:B769 – share some genetic code, even though the former triggered the green notches and exclamation marks, and the latter didn’t. I can’t explain the disparity, other than to float the idea that these patches of data emanate from heterogeneous sources; your comments and conjectures are welcome.

And last and numerically least, cells B770:B777 revert to duly certified date format. Once you’ve unified the date format throughout the Date range and you can rev up the pivot tables and attendant date groupings, etc.

A few codicils: you’ll need to either delete the data-source attributing rows 778 and 779 or splay 777 and 778 with a blank row, thus exiling these extraneous text entries from the greater body of data. There’s also the matter of those month names gathering in the A column. I’m not sure what forthright advantage redounds to these unalloyed text data; we can already chisel months from the date data in B, after all. If for some reason you wanted to groups months qua months, absent their association with their respective years (e.g. the RPI averages for all Aprils), you could go ahead with the B-column data.

Of course the larger question is to ask why they data were compiled in the way in which they were, uncombed and contrary. I don’t know, and short of braving a query to the folks at the Guardian, the evidence suggests a polyglot workbook glued from shards of data prospected from hither and yon. The aim, again: get all the data to speak the same language. Esperanto, anyone?

The cost of living is in the news in the UK but it always is, in one or other of its ubiquitous, chameleon guises; and no less chameleon are the means for measuring that essential but quicksilver property of the commonweal, sometimes called by a less fetching name: inflation.

UK officialdom frames two principal indicators that strive to realize the cost-of-living snapshot – the Retail Price Index (RPI) and the Consumer Price Index (CPI). That plurality of course points to two different stats, measuring two different batches of variables that conduce towards two different numbers (for some definitional distinctions see the Wikipedia discussions here; and look here for a UK-government elucidation of the differences. Note as well the Guardian’s extended discussion of the definitional movement within the RPI and CPI. Thanks to the Guardian’s Charles Arthur for the heads-up. Correlations of the two measures need to take these understandings into account.)

In that connection the Guardian has released its own set of the numbers in spreadsheet mode, these tracking monthly RPIs and CPIs since their respective inceptions, along with a third metric, the Change in weekly pay over 12 months, which considers the relative movement in workforce wages. It’s available here in Excel guise:

inflation uk

(Again, there’s a need to own up to the obvious: namely, that spreadsheets merely acquiesce in the values they receive, without presuming to adjudicate their meaning and validity. That central matter is properly left to a more searching look at the cost-of-living idea.)

In any case the data read more-or-less straightforwardly, and we can proceed with something simple, say a set of correlations of the RPI/CPI/Change in weekly pay fields. RPIs tend to point notably higher than CPIs (again, a close analysis of that discrepancy appears in the government document referenced above), but a high correlation, between the two if obtaining would at least suggest some comparative constancy. Because correlations match pairs of values and because the CPI doesn’t appear on the statistical landscape until 1956, our correlation needs to start at row 489, at which the CPI debuts. In a blank cell enter

=CORREL(B489:B777,C489:C777)

I get .758, a high association by social-scientific expectations, but one clearly ridden by a measure of slack between the two fields. But again, RPI and CPI aren’t measuring precisely the same thing.

We can next move to correlate RPI and then CPI with Change in weekly pay, the latter parameter settling into the sheet at row 633 and descending to row 774, or the October 2012 index. To correlate RPI/Change, enter

=CORREL(C633:C774,E633:E774)

Both ranges (or arrays, to use the technical term) pull up here at row 774, as they must submit the same number of records. Result: .235, a moderate positive association between Retail Prices as operationalized here and Weekly pay.

For the CPI/Change correlation write

=CORREL(D633:D774,E633:E774)

Result here: a notable, but deceptive, -.338.

Deceptive, because a negative correlation typically denotes a degree of reverse trending – when one array’s values move up the other presses upward. But chart the CPI/Change data and we see a fairly orderly covariance:

The “problem” is that the arrays change places around May 2008. From there on, weekly pay falters behind the CPI, at least by and large; and it’s that reversal that spurs the negative correlation. In other words, the CPI and wage figures tend to move in rough concert throughout, but the switch in the higher-lower relation drives the negative correlation. If you don’t quite appreciate that nuance – and I sure didn’t at first – correlate these values:

Result: -.515.

There are some additional simple vantages to gain on the data, namely the monthly ratios and absolute differences between the RPI and CPI.  Move over to a blank area in the sheet – let’s say the G column, and title it Dates on row 488 (because the CPI data commence at 489), and name H488 Ratio. Simply copy the dates starting at B489 beneath the Dates heading, and write in H489

=C489/D489

and copy down the column. That’s simple enough, but instructive just the same. RPIs generally exceed CPIs, a matter of not inconsiderable political import, but we see the ratios careen all over the place, as exemplified by this Cro-Magnon but serviceable chart:

There was, as we see here, a stretch of months in 2009 when the RPI actually fell beneath the CPI.

If we title I488 Difference and compose the even simpler

C489-D489

in I489 and copy all the way down and chart the results, you’ll get something like this:

No shortage of variation here, and worth marking in light of government observation that

“Between 1989 and 2011 Retail Prices Index (RPI) inflation tended to be around 0.7 percentage points higher than Consumer Prices Index (CPI) inflation on average.” (Extracted from the document hyperlinked above). Maybe so, but the constituents of that average run riot across the years.

OK – But I’ve remained eyebrow-raisingly silent about the Date column and those green-notches commanding many – but not all of its cells. Some formatting issues in there? For sure. Not to worry, though; I’ve got you in mind – in Part 2. Be there – aloha.

I’m a legal alien, which means that my star-spangled passport gets stamped in Heathrow these days at journey’s end; it’s what happens when you marry a Londoner and move to her side of the pond. But I can still access scads of demographic data about my country at

http://factfinder2.census.gov/faces/nav/jsf/pages/index.xhtml

and so can you, even if Uncle Sam won’t cough up that green card.

Once you’re onsite, a variety of access routes to the data point themselves at you, guiding the way with signposts of variable clarity; and once you get where you want to go the data beckon to be downloaded to one of a range of formats including Excel, and that’s where we come in. Now prepare to be disturbed.

What do I mean? To appreciate that caution, let’s download this workbook, which details the demographics of the 10023 zip code on Manhattan’s Upper West Side:

 ACS_11_5YR_DP0210023

Put the data in (what appears to be) the E column in your sights and consider the numbers there: that tell-tale left alignment, their upper-left cell corners discreetly festooned with that green indicator and companion exclamation-marked alarm, boding trouble:

Click the mark, and Excel proceeds to confirm your disquiet: these are numbers manqué, valueless, textual interlopers who can’t be added, subtracted, or pivot tabled – at least not yet. To date, every Census workbook I’ve downloaded – a paltry numerator juxtaposed atop the whole, to be sure – freights its numbers with the same impairment, and I don’t know why.

But help is available. You could select the entries in the E-column and click that exclamation mark, divulging the Convert to Number option:

 A click there should restore the data to quantitative form. (You could also select the cells and click Number in the drop-down menu in the Number button group on the Home tab.)

But it’s fit and proper to ask why we’re bidden in the first place to apply remedies to a data-management issue that should have been pre-empted before it hit our screens.

And there’s more. I seem to have placed the above-referenced text/value data in the E column to date, but I’m not too proud to admit I’ve been wrong. The name box in the above shot identifies the selected cell as D10, even as the Alignment button group supplies notice that D10 has been merged. And it has; in fact cells D7 through D199 have amalgamated with the corresponding, same-row cells in the E and F columns, and again I remain mystified by the procedure. It’s possible that a wish to center the title in cell D7 across columns D through I inspired the merge, but that title yet clings to its default left alignment, and there appears to be no need to have extended the merge motif to the cells beneath it. No pun intended, but where’s the justification? Note as well the merge of the text-laden content in what were singly B3 and B4, along with the no-less-curious merge engineered in B210.

The suspicion, then, is that these data have crossed the transom from some other application, and suffered the proverbial loss in translation as a result. The suggestion, then, is that the sheets should have submitted to the necessary retooling before they backed into the web site. (And yes, I’ve seen the merge problem in another Census sheet, too.)

Note also the Wrap Text jag by which the sheet seems to have seized. It appears as if every data-bearing cell has capitulated to that tweak, and some cells have submitted both to Wrap Text and Merge & Center, and I don’t even know what’s supposed to happen to the data when that tandem strikes. What we see, however, is that cell I8 – both merged and wrapped – appears to us as Percent, when in fact the entry really states Percent Margin of Error. Check the Formula Bar.

All of which stirs perhaps even a larger question, one you – and the Census Bureau – may deem unfairly posed. Does any profit accrue to downloading the data in spreadsheet form, in view of the way they’re organized on this and the other Census sheets I’ve viewed? The Census download options include PDF mode – a proposal to which you’d reply: ah, but saving to PDF means you won’t be able to do anything with the data. That’s basically true, but you need to ask what you’ll be able to do in any event, even when it’s Excel that incarnates the data. Study the workbook and think about where you’ll be able to take the data next. Here fertility data are arrayed with household, marital status, and school enrollment figures, and quite apart from the itinerant blank rows, and total rows that cause the kind of redundancy problems I recounted in last week’s post, it’s proper to wonder where the data can go next. I’ve asked the question in an earlier post, but I’ll issue it anew: where can you take the sheet from here?

An unfair question? Perhaps it is. It may suffice to read the data and learn from them, and that’s fine. There’s a great deal in the Census site to learn. But a spreadsheet is an admirably unstable thing; prime its data properly and it can potentiate into something new and instructive, something that wasn’t there before. Is it treasonous, then, to allow that the Census data – at least the data I’ve seen – won’t allow that to happen?

There’s no room for the obvious in the gender reportorial space. If you want to write comparatively about what’s happening in there – and talk about gender is by near-definition comparative – you need to insist upon the data with which to appoint the space; and the gender-parsed data about college enrollments makes for interesting furnishings.

True, the outsized relative female presence in American colleges might by now qualify as an obvious datum all its own, but I have one more comparison in mind – the remarkable, parallel likeness in the breakouts of the numbers for universities in the United Kingdom, filed by the Guardian and transposed to Excel form here:

 The gender gap at universities

(N.B. I’ve supplemented the original workbook’s Higher Education Institutions sheet with a Country field; it is, after all the United Kingdom. And NI stands for Northern Ireland.)

Women comprise about 57% of college/university students in the States, an advantage that appears to have stabilized across the past decade, itself something to think about. The female proportion in the UK stands at about 55% (and last year one-third more women applied to university than men, striking a virtual identity to the 57-43 US split), an altogether striking bit of social homology. After all, who would have confidently imagined a concurrent lurch in the respective gender ratios, a shared velocity of change rambling across the two countries -even granting their real but limited cultural affinities? That the two gender tempos (all right, all right – I almost went with tempi) appear to have marched to the same metronome 3500 miles apart is no truism, but rather a provocative, newsworthy conjunction, worthy of a sociological grant or two. But I do go on.

In any case, on to the data, which stream across four worksheets and throw out some issues on which you’ll have to do your due diligence. Click through the numbers and it becomes clear first of all that they’ve been rounded off, for reasons to which I’m not privy; and while that discrepancy – and that is what it is – doesn’t subvert the larger enterprise, it’s a touch bothersome.

Now tap into the Higher education institutions tab, and onto the formula in cell F3:

=SUM((C3/E3))*100

The 100 serves to aggrandize the formula results beyond zero, e.g. 61.9 rather than .619 or 61.9%. But the SUM prefix and attendant parentheses bring nothing to the expression, which thus should have been rendered:

=(C3/E3)*100

The same critique can be levelled at the percent computations prowling the Qualifications by gender subjec [sic] sheet. (Note by the way the truncated “subject”, a casualty of Excel’s 31-character naming limit on worksheet tabs, a condition which does not beset the original, Google-docs platformed sheets. Note a similar forced abridgement of the Class of degree, by ge [sic] sheet title. You’ll thus probably want to rename these gnarled identities.) And note as well the intermittently hard-coded data fields across the workbook (as with the percentage data in the Students obtaining undergraduate [sic] sheet], fields which submit to formulaic treatment in other sheets. I can’t explain the inconsistency.

But you’ll have to save the heavy-duty emending for the Class of degree obtained sheet:

If you want these data duly prepped for pivot tabling, etc., you’ll need to

1. Delete row 4, mischievously interpolated between the data and their titles
2. Do something about the Female, Male, and All Genders identifiers (curious adjective here, “All”; how about Both?) posed as outline headings – namely, by lowering them into each record and paring any resulting blank rows:

And as you’re by now expert pivot tablers, you can let your spreadsheet imagination run riot with the data.

But let’s cut back to the Higher Education Institutions sheet. Suppose you want to call upon a pivot table to say, break out the gender enrollment data by Country (remembering that the data confine themselves to full-time students). First, insert a row between the last university record – University of Ulster – and the Total UK row, thus distancing the latter from any imminent table. If you don’t, Total UK will factor itself into the pivot data, inflicting a debilitating redundancy upon the table – because the totals aggregate all the data above them – in effect, summing the data twice.

Next, populate the pivot table:

Row Labels: Country

Values: % female full-time undergraduates

% male full-time undergraduates

Country

Summarize the quantitative value fields by average, and format decimal points to taste (I’ve stipulated two such points).  You should see:

(I’ve also fiddled with column widths.) These findings average the averages; that is, they impart equal weight to each institution’s gender percentages irrespective of institution size, a salient measure for some purposes that nevertheless won’t figure women’s overall, actual enrollment proportion. In order to achieve that measure drag the current value fields off the table and slide in the Number of female and male f/t undergraduates:

(And you’ll want to bag those Grand Total decimals.) Now here’s the issue. Clicking PivotTable Tools > Options > Show  Values As > % of Row Total will consider the female and male fields separately, and as such won’t deliver the comparative, cross-row percentages you’re seeking:

And that’s because the % of Row Total capability only threads across values of the same field. Had the data installed a Gender parameter instead comprising female and male values – that is, had it headed a column called Gender comprising successive enrollment number records for F and M, for example – the percentage of row totals could indeed obtain. In our case, however, you’d need to resort to the kind of Calculated Fields I detailed in my September 6 post, in which a new, pivot-table-specific formula would have to divide say, the female undergraduate field by the sum of female and male undergraduates fields. It’s doable to be sure, and sometimes necessary, but it’s messier.

Yeah – fields and values. You gotta nail that distinction down – even if the spreadsheets you have to deal with don’t.

It’s a man thing, this problem with following instructions, but if I’ve guessed right, the NCDC temperature spreadsheet on which we’ve been working should look something like this right now, in excerpted form:

And you can get what you see above here:

NCDC temperature stats 2

(By the way, ignore those green markers clinging to the upper-left corners of the Code cells; they signal a Number Stored as Text “error” message, a state of affairs we actually desire here, and one accounted for in last week’s post. In addition, you don’t need to introduce decimal-point consistency among the temperatures right here; since these are to be shuttled into a set of pivot tables, the pertinent formatting can be carried out there.)

You’ll recall I closed Part 1 with the gentle augury of more tweaks to come, and I don’t aim to disappoint. I’m proposing now that we thread in still one more column, to be interposed between C and D and named Area Status. In what is now D2 enter

=VLOOKUP(LEFT(A2,3),Areas,3)

An expression that looks up the kind of area embodied by the data in the C column, e.g., Alabama is a State, and the Soybean Belt is a…Belt. And why do we need to know any of this? Because a mass pivot tabling of all the records – that is, a wholly inclusionary tabling of each of the 11564 records, needs to come to terms with the overlapping character of those areas – but it won’t. The Eastern Region, for example (code 121), comprises a zone of 16 proximate states (see the NCDC Read Me page I referenced in last week’s post for an enumeration of these, along with some methodological morsels that won’t make their way into the popular press); and batching these among the individual state data is tantamount to counting the same data twice, or perhaps even thrice, a messy glop of redundancy that’ll throttle any and all attempts at analysis. We need Area Status, then, the better to filter one status or another at a time – to properly curtail our gaze to only state, or only regional data at one time.

And last, and very possibly least, flash over to the Q column and enter, in Q2:

=AVERAGE(E2:P2)

That recommendation is fairly straightforward. We want to be able to return state/regional averages by year, I think, and that deed is now hereby done (note I’ve formatted the averages to two decimal points). (You might, however, want to think about how a design alternative, whereby the 12 month columns or fields could be piled into one, unitary Month field, would serve the data. It’s true, of course, that you’d be pumping 12 times as many records into the source worksheet – one record for each state/region, year, and month – and 120,000-plus rows of data might bring your computer’s processor to its knees. Nevertheless, other explicative gains could be realized as a result, because as the data currently stand, each month field has to be wheeled into the pivot table separately – and because you’d sooner or later want to aggregate the months into yearly composites, things start would start getting labor-intensive as a result. Hence my AVERAGE field, which does some of that aggregating work before the data reach any pivot table.)

Now once all the fields have been tilled you can begin to do the pivot table thing, starting with some of the standard come-to-mind orchestrations, e.g.

Report Filter: Area Status (click State)

Row Labels: State/Region (these will return only state names at the behest of the Report Filter State selection above).

Column Labels: Year. These data could, in the interest of a visual streamlining, be grouped by say, 5-year intervals, thus pinching 118 columns worth of years into 24.

Values: Average (these values to be summarized by Average).

These outputs could then be nicely Sparklined (remember them? See my November 29 post), e.g., this excerpted shot of a few of the state trajectories (the shot takes advantage of the Freeze Panes > Freeze First Column option posted to the View tab:

(Note that you’d want to turn off the grand totals for rows here (PivotTable Tools > Design > Grand Totals in the Layout button group), because those aggregated data would be read by the Sparklines as just another yearly data point, and they aren’t.)

What you should find, across the pivot table permutations, is a broad if not wholly ineluctable upwards angling in temperatures – as expected, of course, but I’m prepared to believe there are plenty of nuances among the numbers.

So there you have it. Everyone talks about the weather, so now go do something about it – or at least do something with it.

Last week’s meteorological revelation about 2012 – its one-degree edging of the previous annual US average temperature high – received its just media due, adding one more metaphorical log onto the fire of controversy about global warming (though the New York Times article linked above equivocates about the evidentiary conclusions). Those on the lookout for some hard substantiating numbers can tune into the National Climatic Data Center (NCDC), more specifically this file:

ftp://ftp.ncdc.noaa.gov/pub/data/cirs/drd964x.tmpst.txt

But not to worry; I’ve adapted the above to spreadsheet form here:

NCDC temperature stats

(Two notes: this spreadsheet updates an earlier version. And note the lookup table I’ve manufactured for the Areas Lookup sheet, range-named Areas. We need to get to this later.)

We can register a few conjectures about what we might want to learn from these data – say, a breakout of monthly temperatures by years or groupings of years and/or states (the 48-contiguous ones, that is), and perhaps even by coarser, regional rubrics, provided of course those parameters are in there, and don’t worry – they are. And of course you’ll be anticipating a fitful but dogged rise in temperatures across the 118 years’ worth of data, something you should be able to demonstrate or disconfirm here.

In any case, I’ve put the file contents in their pace starting at row 2 because the native NCDC data are headerless, and that just won’t do; you’ll thus want to reserve row 1 for some apt titling.

But first things first; we can’t top columns with headers without columns to top, and right now, and first appearances notwithstanding, all the data are presently crowded into the A column only – because the source file whence the data come is a good old all-American text file, in which the data have yet to be spliced into spreadsheet-friendly columns.  As a result, you’ll need to trot out the Text to Columns option (see my October 11 and 18 posts, which explain Text-to-Columns in some detail); only then, once you’ve safely tucked the data into their respective columns, can you go about heading them all (and you should hold to the Fixed Width default at ticked at Text to Columns’ inception.) Just note something else – you’ll need to depart from the standard Text to Columns run-through in one regard for reasons that should become intelligible a bit later: at Step 3, be sure to tick the Text Column data format radio button for the first incipient column only:

When the smoke clears your sheet should have sawed the data into 13 columns, in which numbers 2 through 13 clearly report monthly temperature data. These’ll naturally be headed Jan-Dec, or something cognate. But it’s column one that holds out the more formidable challenge, and naming it is the least of it.

I was directed by a helpful NCDC tech rep to a site read me file that breaks down the composite contents of those 10-digited data in column one, which I’ll title Code. We’re told:

That is, digits 1-3 attest a state or other regional code, such as basin or shelf (these are enumerated in the accompanying lookup table, and keep those data in mind).  Digits 4-6 are unvarying across all the records, and as such can be ignored (digits 5-6 among our data always yield 02 for temperature, as per the above screen shot).  And digits 7-10 always denote the record’s year, a datum we want to isolate in order to abet various pivot-tabled breakouts and the like. Thus you can insert a column to the immediate right of Code, name it Year, and format the column in Number mode. Why bother with that last step? Because the new Year column will inherit the prevailing formatting of the column to its left – in our case, text – any formula entered in the column will, absent user intercession, degrade into unreconstructed typing – that is, nothing but text.

Then entire this formula in cell B2, which should be copied down its column:

=VALUE(RIGHT(A2,4))

This expression cadges digits 7-10 from A2, etc., streaming the relevant years down the Year column in B (and you’ll probably want to lose any decimal points that may have squeezed their way into the cells). We need VALUE here because that 10-digit code in A2, etc. from which the year has been finessed is text, after all; and VALUE forces numeric status onto numeric-looking data that have been formatted as text.

Next, we’d likely want to supplement each record with the name of the state/region associated with its reported temperatures, and we can do that job by making resort to a relatively uncontroversial VLOOKUP formula. Insert a new column to the right of Year, call it State/Region or some such, and in C2 enter

=VLOOKUP(LEFT(A2,3),Areas,2)

Translated, the expression Identifies the first three characters of any A-column entry, looks these up in the Areas lookup table (again, it’s stored in the Areas Lookup sheet), and returns the appropriate item (e.g., state or region name) from the table’s second column. Copy the formula down the C column.

That looks good, but the issue I raised about 550 words ago remains unrequited: Namely, in the course of conducting the Text to Columns routine why did I insist that we invest the first, Code-bearing column with Text status in the first place?

Here’s why: left to its default devices, Text to Columns will format its columns in General mode – meaning that for each column Excel will try to determine the data type befitting the data therein. And by default Excel regards the first column – the one we’re calling Code – as a numerical field, and thus will, for example, streamline the very first Code:

0010021895

to look like this:

10021895

Because Excel deems the first two characters as leading zeros – numerically meaningless frippery – Text to Columns simply throws them out, leaving us with an 8-digit code for Alabama, and labelling its state identity 1, in lieu of the original 001. But New York, coded 030, suffers a loss of but one leading zero, and its data are thus remaindered into a 9-digit value. And the Eastern Region – code 121 – hoards all 10-digits, and all this digital disparity causes big problems for the VLOOKUPs – not insurmountable ones, mind you, but the round of additional hoop-jumping required to set all the data straight isn’t worth the bother. But once we format the Code data column into text form, thus overruling Excel’s General default, each record preserves its original 10-character span, and frees us in turn to invoke the 3-character state codes in every case – a more consistent take on the data.

And yeah – there’s a bit more tweaking to be done, but once my word count hits four figures I know the natives get restless, and the collective slosh of watering eyes gets disconcerting on this side of the lectern. I’ll close this post, then, with a different kind of question, this one historical: you’ll observe that the temperature data for Arizona (002) dates back to 1895, as it does for all the other states. Yet Arizona did not enter the Union until 1912, a point I raised in an email to the NCDC. Meteorologist Mark Seiderman got back to me quickly, noting that data were nevertheless tracked in Arizona in its pre-statehood phase, but at a lower “station density” – meaning fewer readings were taken.

OK, that’s it for today; meet me at the rathskellar in a half-hour.

As I’ve put myself on a limited work schedule owing to a routine medical procedure (which has been already carried out), I’m recusing myself this week from a post. One correction, however: I had replied to commenter Doug Glancy (The Camera Tool, Part 1 post) that the Camera button has been installed as a default on the Quick Access Toolbar in the Excel 2013 beta. That isn’t true.

By the way, the 2013 release (which you can freely download here) features a Recommended Pivot Table button which when clicked opens this window, the recommendations forged from the data with which you’re currently working:

The recommendations may range from inspiring to clunky, and won’t absolve you of the mandate to learn pivot tables, though.

Consider this tableau:

And then this one:

(Note: the above shot is an update; see Kristen Long’s comment below.)

You’ve seen tableau one, a word (or tag) cloud, before, a now-standard, next-big-thing journo tool, this one floated into the firmament by Kirsten Long of the Politico web site.

Tableau two scrapes the same data – the text of President Obama’s September 8 jobs bill exhortation – but here makes primitive resort to your correspondent’s key-word spreadsheet  (which I continue to refine), introduced in the previous post.  The obvious question, then: how do the two modes of presentation compare?

Sure – you’ll accuse me of irredeemable, self-leaning bias, and I’ll have to take that hit; and while I’m at it, I’ll add another, incriminating mea culpa: I don’t think well visually, either.  Ok, then; that means you’ll have to humour, or even better, patronize, me as we move along. But hey – it’s my blog.

But enough about me. We know perfectly well what it is the cloud means to tell us, but

1. With what precision is relative word incidence conveyed? It’s clear the cloud invokes two presentational parameters – word size and shading, in the service of the comparisons, and are we entitled to assume as a result that  sizing is properly proportioned, i.e., does a word appearing 12 times in the speech grow twice as large as a word appearing six? And how do the blacks and grays comport with one another?  I see no apparent rule at work for daubing this or that hue across this or that word. Perhaps there is no rule, and the colors merely subserve some fetching aesthetic variety. But is this something about we should be wondering?
2. More subtly perhaps, we could ask as well about word positioning. It’s clear that the words above are not made to stack in upright, size-hierarchical relation, but if not that, then what? If the design intent is merely random, ok – but what then do we make of that presentational gestalt, and its news-informational value?
   1. The word cloud conceit surmises a way to look at categorical data – essentially qualitative information, of the classic gender-religion-ethnicity stripe. These data can’t be directly scaled – maleness can’t be “more” of anything than femaleness – though of course they can be counted.  Here the data are words, and because they aren’t mapped to either of the great existential properties of space or time – that is, they aren’t forced into place – the words can prance anywhere across the viz, owing to designer discretion. By way of counter-example: a data viz of crimes mapped to latitudes and longitudes necessarily slots the crimes into the coordinates at which they’ve been perpetrated. Word clouds incur no such compulsion, thus vesting placement decisions in the designer alone. Where, then, do the words go? The point is that they can go anywhere – and that is the point of the question.

My prosaic little spreadsheet-driven word count, on the hand, does just that – it counts word frequencies rather determinately, and sorts them too. Pushing the matter to the retro breaking point, you could even do this:

Now that’s not cool. But what does the reader want and need to know?

There’s something curiously interstitial about word clouds. Driven by a thrall with word frequencies – typically the province of academics and game designers – the clouds yet give pride of place to the imagery festooning the data. We’re given a beautiful arrangement of nuts and bolts – but for whom?

Do a Google Images search for word clouds and you’ll see what I mean. Or wend your way to any of the word cloud-construction sites – e.g., wordle, tagxedo, worditout, etc., and check out the possibilities. It’s fun to make word clouds, and there’s nothing wrong with that – but what are journalists doing with them?

True – Kristen Long’s cloud is a good deal more sober that those espoused by the novelty sites, and it delivers its macro point, to be sure. But don’t the basic informational questions remain there to be asked? (Also look at Wikipedia’s examples in its entry on clouds, including a nice key-word comparison between George Bush’s 2002 state of the Union speech and Barack Obama’s 2011 oration, the words sorted in alphabetical order.) How do clouds contend with the demands for reportorial precision?

Needless to say, all of the above points to the much larger question about the visual portrayal of data that might be otherwise delivered through more plebeian means, e.g., spreadsheets. Sorry – I can’t answer the question here, only ask it. But are journalists – properly seeding the clouds?